Этот урок курса является факультативным или дополнительным. Для его усвоения необходимо понимать основы двоичной системы счисления, уметь переводить числа между системами счисления, а также знать, что такое битовые или поразрядные операции. Ознакомиться с последними можно в этой лекции.
В языке программирования C доступны следующие поразрядные операции: & (И), | (ИЛИ), ^ (исключающее ИЛИ), << (сдвиг влево), >> (сдвиг вправо) и ~ (поразрядное дополнение до единицы). Давайте рассмотрим их на примерах, но сначала остановимся на том, как выводить числа в других системах счисления на языке C.
В языке C можно присваивать целые числа в десятичной, восьмеричной и шестнадцатеричной системах счисления. Чтобы указать число в восьмеричной системе, перед ним ставится 0, а для шестнадцатеричной — 0x, например:
int a, b;
a = 077; // восьмеричное число
b = 0x1F; // шестнадцатеричное числоВыводить целые числа можно в десятичном, восьмеричном и шестнадцатеричным формате. Вот пример вывода двух переменных в этих форматах:
printf("%d %o %x %X\n", a, a, a, a);
printf("%d %o %x %X\n", b, b, b, b);На экране вы увидите:
63 77 3f 3F
31 37 1f 1F
Восьмеричные и шестнадцатеричные системы полезны, так как они упрощают работу с двоичной системой. Каждая цифра восьмеричного числа преобразуется в три двоичных цифры, а шестнадцатеричного — в четыре. Вот таблица соответствия цифр восьмеричной системы двоичным числам:
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Если у нас есть восьмеричное число 037, то в двоичном виде оно будет 011 111, как видно из таблицы.
- Как будут выглядеть восьмеричные числа 04271 и 03566 в двоичном представлении?
- Составьте таблицу перевода шестнадцатеричных цифр в двоичные числа. Переведите числа 7D, FFFF, 2C9 в двоичную систему счисления.
Если бы битовые операции проводились с десятичными числами, то каждый раз понадобилось бы конвертировать их в двоичную форму, что не всегда удобно. В то же время, представление восьмеричных чисел сразу передает двоичный эквивалент, что сокращает необходимость в постоянных пересчетах. Видя число 017, можно представить, как четыре последние бита памяти заполнены единицами.
Давайте перейдем к исследованию поразрядных операций и протестируем их. Вот пример программы:
int a, b;
a = 017;
b = 036;
printf("0%o & 0%o = 0%o\n", a, b, a & b);
printf("0%o | 0%o = 0%o\n", a, b, a | b);
printf("0%o ^ 0%o = 0%o\n", a, b, a ^ b);
printf("0%o << 2 = 0%o\n", a, a << 2);
printf("0%o >> 2 = 0%o\n", a, a >> 2);
printf("~0%o = 0%o\n", a, ~a);Работа программы даст следующий результат:
017 & 036 = 016
017 | 036 = 037
017 ^ 036 = 021
017 << 2 = 074
017 >> 2 = 03
~017 = 037777777760Чтобы лучше понять этот результат, взгляните на иллюстрацию ниже:
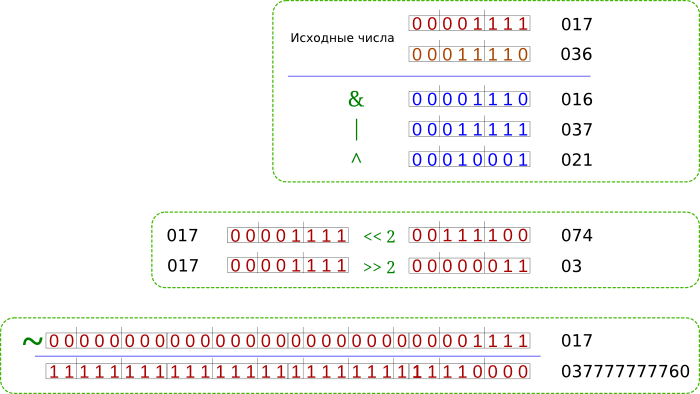
Почему получилось такое большое значение в последнем случае? Потому что под целые числа в форматах %d, %o, %X выделяется целых 4 байта памяти.
- Используйте шестнадцатеричные числа для создания аналогичной программы. Поясните её результаты.
- Экспериментируйте с составлением сложных битовых операций и анализируйте их результаты.
Рассмотрим пример использования битовых операций. Представим, что у нас есть массив и мы хотим определить его "маску", отражающую позиции отрицательных и положительных элементов. Здесь единица (1) будет означать положительный элемент, а ноль (0) — отрицательный. Например, если массив выглядит так {4, -3, 2, 2, 8, -1}, то его "битовая маска" будет 101110, что в восьмеричной системе равно 056. Следующий алгоритм поможет решить эту задачу:
- Пусть массив состоит максимум из 32 элементов, и для его "маски" достаточно переменной типа
int, назовем её mask, в которую запишем начальное значение 0. - В цикле
forобходим элементы массива. При нахождении положительного элемента устанавливаем соответствующий ему бит в mask в 1. - Вывести значение mask в восьмеричном виде на экран.
Как установить определённый бит в 1? Каждый бит в числовом представлении имеет аналог среди степеней двойки. Например:
20 = 0000 0001
21 = 0000 0010
22 = 0000 0100
23 = 0000 1000
24 = 0001 0000
и так далее. Если эта последовательность ещё не усвоена, пересчитайте её. Если применить к переменной mask операцию побитового ИЛИ (|) с соответствующей
степенью двойки, то устанавливается один бит в 1. В примере:
(0) 0000 0000 | (25) 0010 0000 = 0010 0000
(32) 0010 0000 | (27) 1000 0000 = 1010 0000
Обратите внимание, что первый элемент массива с индексом 0 должен соответствовать биту, находящемуся в начале двоичной маски. Зная количество элементов массива (N),
степень двойки определяется формулой N - i - 1. Например, для третьего положительного элемента в массиве из 10 элементов
устанавливается восьмой с конца бит, что значит второй операнд для ИЛИ будет 27.
Как возвести число в степень на языке C? В C возможны операции приведения типов, которые изменяют тип переменной. Стандартная библиотека math.h предлагает
функцию pow(), возвращающую число, возведённое в данную степень. Несмотря на её вещественный результат, он может быть преобразован в целый с помощью
(int) a. Программа может выглядеть так:
#include <stdio.h>
#include <math.h>
#define N 12
main () {
int nums[N] = {7, 3, 9, -5, -3, 2, 1, 0, 16, -4, 2, 0};
int mask = 0, i;
for (i=0; i < N; i++)
if (nums[i] >= 0)
mask = mask | (int)pow(2,N-i-1);
printf("%o\n", mask);
}
Напишите программу, описанную выше, и исследуйте, как она работает1. Подумайте, как можно вывести на экран двоичное представление восьмеричного числа и
попробуйте это реализовать.
1 Если возникают проблемы с компиляцией, добавьте к вызову gcc опцию -lm (например, gcc -o
bits bits.c -lm).